Unii susțin că datorăm matematica pură lui Pitagora, cel care mai este numit și primul matematician „adevărat”. Chiar dacă celebrul filosof și matematician grec rămâne o figură controversată, astăzi, suntem beneficiarii minții sclipitoare a lui Pitagora.
- Pitagora s-a născut în secolul al VI-lea î.Hr, pe insula Samos din Grecia. Este considerat întemeietorul pitagorismului, care punea la baza întregii realități, teoria numerelor și a armoniei. și cel ce a descoperit teorema geometrică și tabla de înmulțire, care îi poartă numele.
Pitagora nu a lăsat nicio scriere matematică și o mare parte din ceea ce știm despre gândirea pitagorică provine din scrierile lui Philolaus și ale altor cărturari pitagorici de mai târziu. Chiar dacă unii nu sunt convinși că unele teoreme atribuite lui nu au fost concepute cumva de elevii săi, influența lui Pitagora continuă să fie resimțite astăzi, la mai bine de două milenii și jumătate după moartea sa.
Teorema lui Pitagora
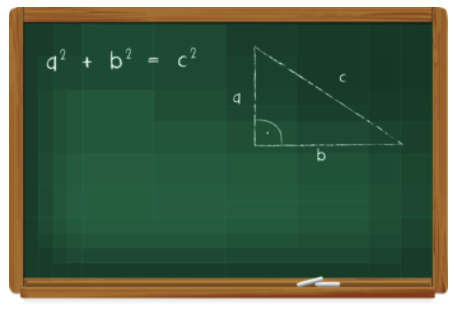
Deși a fost folosită și în Babilonul antic și China, meritul pentru demonstrarea teoremei a fost atribuit lui Pitagora și adepților săi.
- Teorema afirmă că în orice triunghi dreptunghic, suma pătratelor catetelor este egală cu pătratul ipotenuzei. Această teoremă nu este doar baza pentru trigonometrie, ci și o modalitate de a conecta geometria și algebra.
Mai mult, potrivit profesorului David Joyce de la Universitatea Clark, teorema poate fi extinsă dincolo de calculul triunghiurilor și poate fi utilizată în domenii variind de la astronomie la construcție și chiar la rețelele sociale, făcându-o cu adevărat o teoremă cu utilizări la scară globală!
Descoperirea numerelor iraționale

Teorema nu a fost singura contribuție semnificativă atribuită lui Pitagora. În timp ce atenția oamenilor se concentra în jurul numerelor întregi, perfecțiunea, incompletul, urâtul și frumusețea, au putut dovedi – spre disperarea lor – existența numerelor iraționale.
Această descoperire a trimis valuri de șoc în toată societatea, producând ceea ce s-a numit „primele crize în matematică.” A fost considerat un punct major de dispută în cadrul școlii pitagoreice, deși mai târziu matematicienii aveau să ajungă să aprecieze importanța numerelor iraționale atunci când efectuau un complex de ecuații matematice. Cu toate acestea, la acea vreme, aceasta descoperire a numerelor irațioanle contrazicea o convingere profundă conform căreia existau doar numere „pure”.
Studiul Cosmosului

Elevii școlii lui Pitagora credeau că armonia și echilibrul în toate lucrurile determinau ordinea cosmosului.
- Pitagora este considerat drept primul gânditor care a crezut că Pământul este o sferă. Cu toate acestea, experții sugerează că teoria sa a avut mai mult de-a face cu credințele metafizice decât cu cele științifice.
Ideile școlii lui Pitagora, care vorbea despre un echilibru între planete care duce la armonie (numită „muzica sferelor”), ar fi fost utilizate într-o oarecare măsură de Johannes Kepler în lucrarea sa „Harmonice Mundi”, sau „Armonia lumilor”, o încercare de a înțelege și a modela mișcarea planetelor din sistemul nostru solar.
- De asemenea, lui Pitagora i se atribuie dovada că steaua dimineții era de fapt planeta Venus, adică nu era deloc o stea.
Crearea scării muzicale

Pitagora și adepții săi sunt, de asemenea, acreditați pentru crearea scării muzicale moderne, folosind teoria numerelor pentru a descoperi cum intervalele cele mai plăcute auzului ar putea fi exprimate în cifre pure.
- Elevii lui Pitagora au descoperit că corzile muzicale de aceeași grosime, dar așezate la rapoarte de lungime diferite, precise, sunau plăcut atunci când erau atinse împreună. Corzile de aceeași grosime tăiate la lungimi care nu respectau acest principiu păreau discordante și produceau sunete neplăcute auzului.
De exemplu, au constatat că un șir de corzi cu o anumită grosime și lungime produc un anumit sunet, în timp ce alte corzi, având jumătate din lungimea celorlalte, produc un sunet similar, dar într-un registru mai înalt. Au folosit rapoartele numerice 1: 2 pentru a reprezenta octava, 2: 3 pentru a reprezenta cincimea perfectă și 3: 4 pentru a reprezenta a pătrimea perfectă, stabilind o bază pentru sistemul modern încă în uz astăzi.
Aceasta a fost scara sonoră preferată în muzica instrumentală a Evului Mediu.
Moștenirea lăsată de Pitagora

Indiferent dacă discutăm despre influența pe care a avut-o Pitagora asupra lumii matematicii, ne concentrăm asupra ideilor sale legate de migrația sufletelor sau dacă luăm în considerare influența pe care ar avea-o (atât pozitivă, cât și negativă) asupra gânditorilor de mai târziu, precum Platon, nu există nicio îndoială că Pitagora și ideile sale inovatoare au ajutat la modelarea modului în care vedem impactul numerelor în viața noastră de zi cu zi.
Și mai important de știut este că, datorită teoremei lui Pitagora, care ne dă posibilitatea de a găsi lungimea unei laturi a triunghiului, date fiind lungimile celorlalte două laturi, deținem o tehnică utilă în domeniul construcțiilor și al navigație.
La ce ne folosește teorema lui Pitagora în viața de zi cu zi
1. Arhitectură și construcții

Pentru că se bazează pe două linii drepte, teorema lui Pitagora vă permite să calculați lungimea diagonalei care le conectează. Această aplicație este frecvent utilizată în arhitectură, prelucrarea lemnului sau alte proiecte de construcție fizică.
- De exemplu, când vreți să construiți un acoperiș înclinat. Dacă știți înălțimea acoperișului și lungimea pe care trebuie să o acopere, puteți utiliza teorema lui Pitagora pentru a găsi lungimea diagonală a pantei acoperișului. Puteți utiliza aceste informații pentru a tăia grinzi de dimensiuni adecvate care să susțină acoperișul sau pentru a calcula suprafața acoperișului pe care ar trebui să o acoperiți cu tablă sau țiglă.
2. Construirea pereților și fundației în unghi dreptunghiular
Teorema lui Pitagora este de asemenea utilizată în construcții pentru a se asigura că o clădire este pătrată. Un triunghi ale cărui lungimi laterale corespund teoremei lui Pitagora va fi întotdeauna un triunghi dreptunghiular. Astfel, constructorii vor ști că își construiesc pereții sau fundațiile pe liniile drepte.
3. Navigație

Teorema lui Pitagora este utilă pentru navigația bidimensională. O puteți folosi și cu ajutorul a două lungimi puteți găsi cea mai mică distanță. De exemplu, dacă vă aflați pe mare și navigați către un punct aflat la 300 de mile nord și 400 mile vest, puteți utiliza teorema pentru a găsi distanța de la nava dvs. la acel punct și a calcula câte grade spre vest de nord trebuie să faceți pentru a ajunge la acel punct.
- Aceleași principii pot fi utilizate și pentru navigația aeriană. De exemplu, un avion își poate folosi înălțimea deasupra solului și distanța față de aeroportul de destinație pentru a găsi locul corect pentru a începe o coborâre către acel aeroport.
4. Topografie

Topografia este procesul prin care cartografii calculează distanțele numerice și înălțimile dintre diferite puncte înainte de a crea o hartă. Deoarece terenul este adesea neuniform, topografii trebuie să găsească modalități de a măsura distanța într-un mod sistematic. Teorema lui Pitagora este utilizată pentru a calcula cât de abrupte sunt pantele dealurilor sau munților.
Un topograf privește printr-un telescop spre un baston de măsurare pe care îl amplasează la o distanță fixă, astfel încât linia de vedere a telescopului și bastonul de măsurare formează un unghi drept. Deoarece topograful cunoaște atât înălțimea bastonului de măsurare, cât și distanța orizontală a bastonului față de telescop, el poate folosi apoi teorema lui Pitagora pentru a găsi lungimea pantei care acoperă acea distanță și, din acea lungime, poate determina cât de abruptă este.








